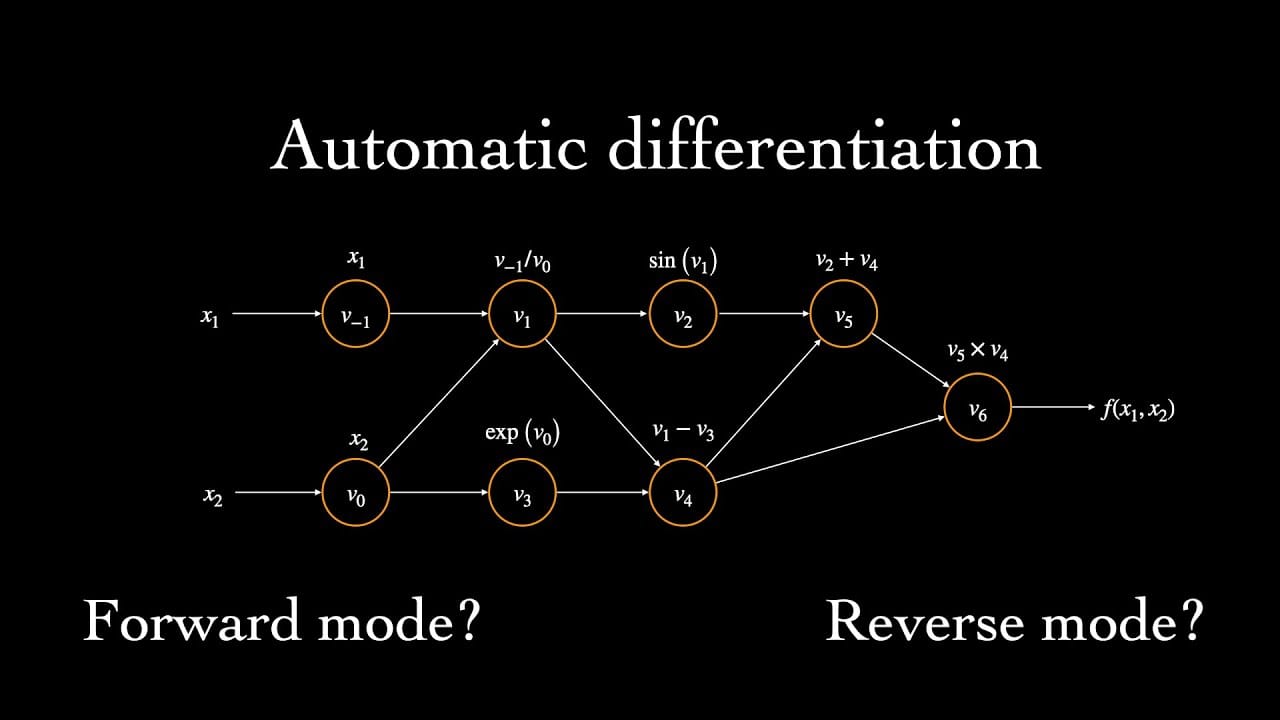
مشتق‌گیری اتوماتیک (AutoDiff) روشی برای محاسبه مشتقات توابع به صورت دقیق و خودکار با استفاده از برنامه‌های کامپیوتری است. این روش با تحلیل مستقیم کدهایی که تابع را تعریف می‌کنند، مشتقات را به دست می‌آورد. برخلاف روش‌های عددی و نمادین، مشتق‌گیری اتوماتیک دقیق‌تر و کارآمدتر است.

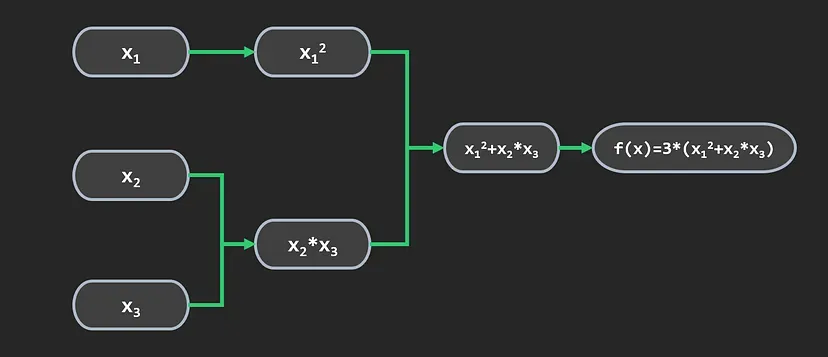
توضیح مشتق‌گیری خودکار با یک تابع ساده

من خودم هنوز این موضوع را در دانشگاه یاد نگرفته‌ام، بنابراین یک ویدیو تماشا کردم و همچنان گیج بودم. اما توضیح بعدی به من کمک کرد تا کاملاً درک کنم:

مشتق‌گیری خودکار (AutoDiff) روشی برای یافتن مشتق یک تابع با استفاده از یک برنامه کامپیوتری است. در نظر بگیرید یک تابع ساده داریم:

f(x) = x^2 + 3x + 5

مراحل در تفکیک خودکار

تجزیه تابع:

   هر عملیات در تابع را شناسایی کنید.

   تابع ما را می‌توان به مراحل ساده‌تر تقسیم کرد:

   1. a = x

   2. b = a^2

   3. c = 3a

   4. d = b + c

   . f(x) = d + 55  

مشتق‌گیری خودکار به روش پیشرو (Forward Mode AutoDiff)

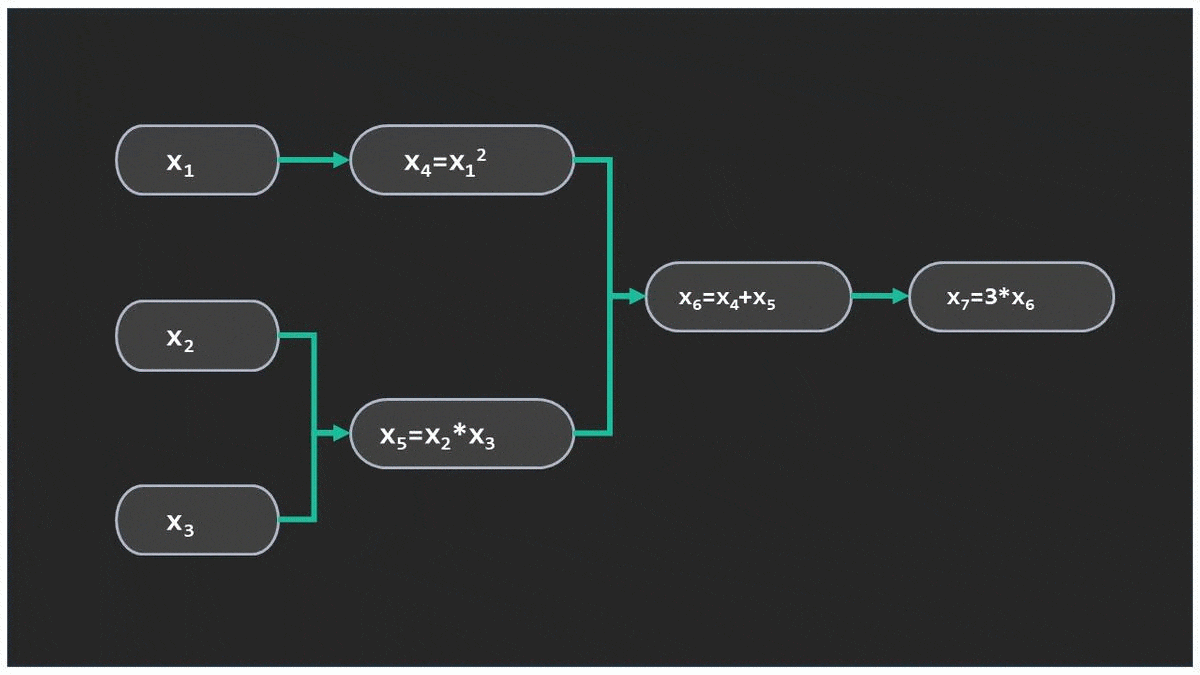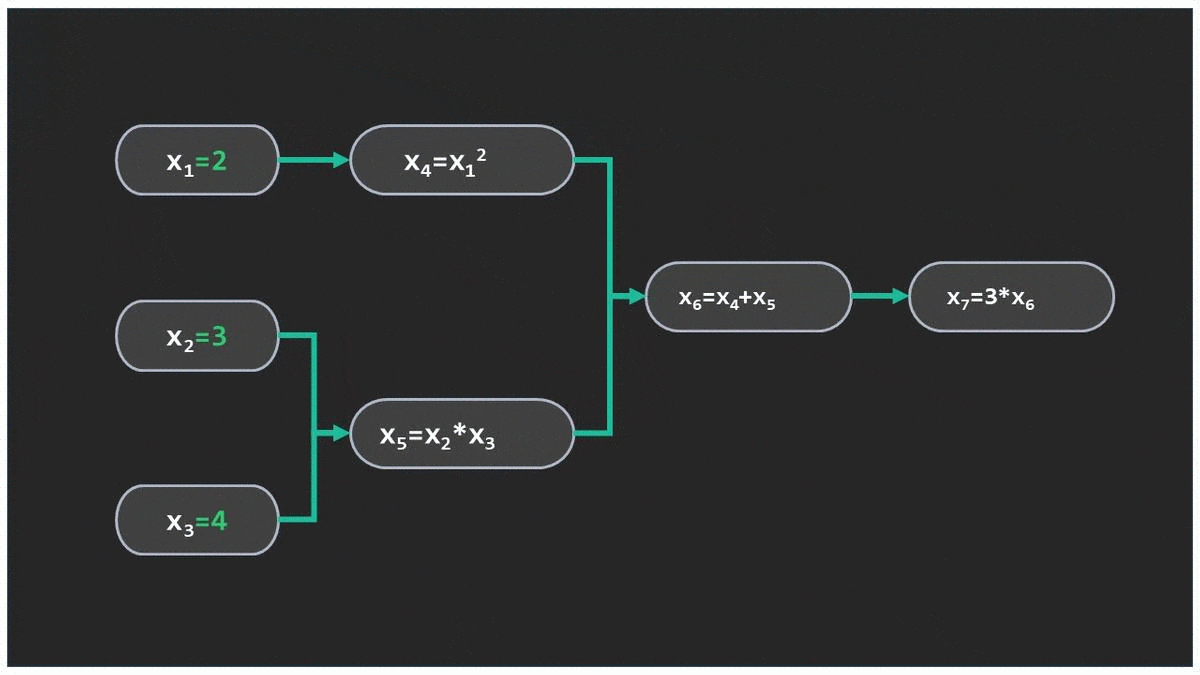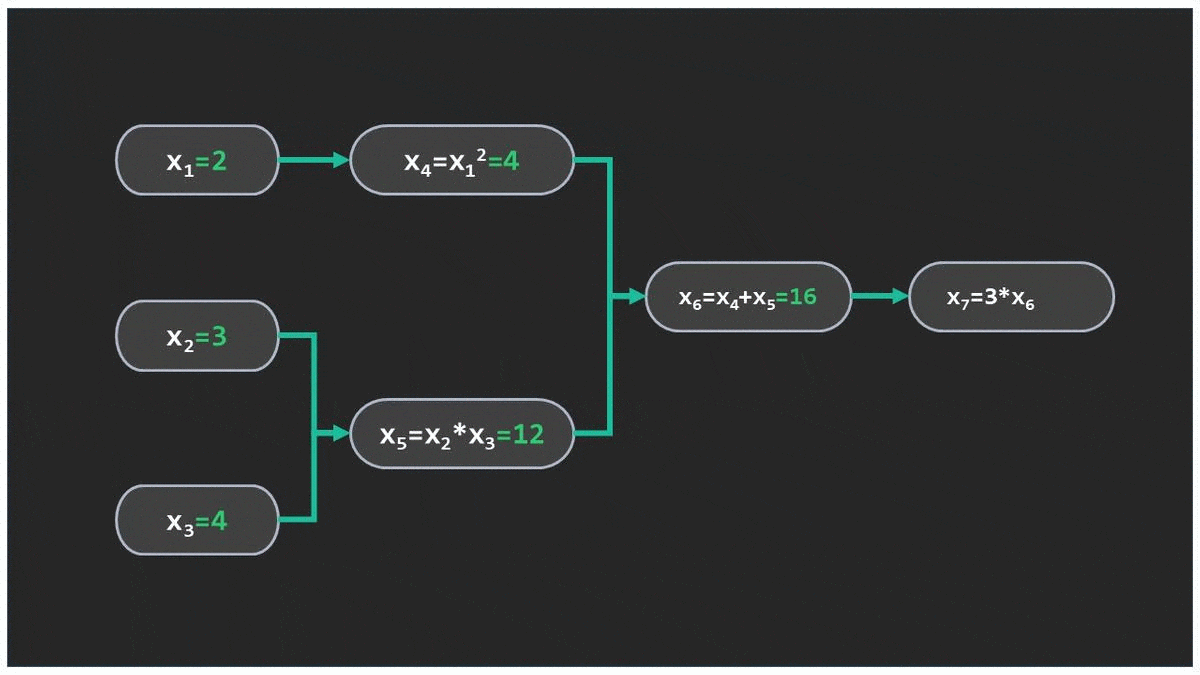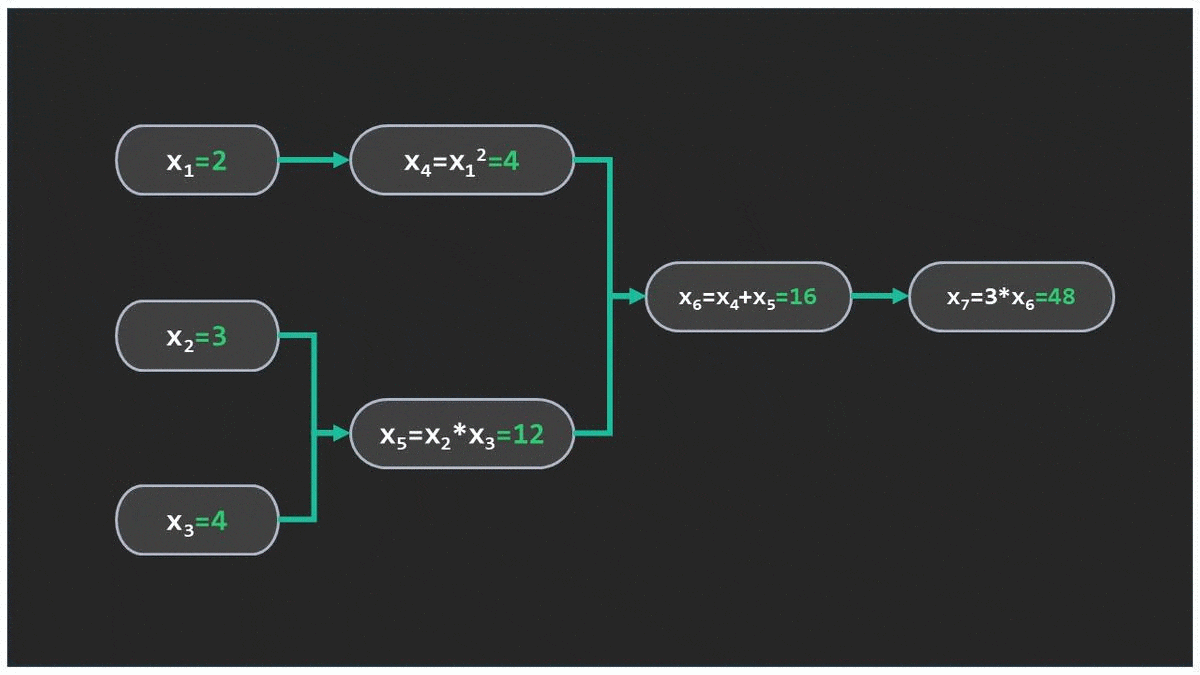
روشی است که با استفاده از آن می‌توان مشتق توابع را به صورت دقیق و خودکار با کمک برنامه‌های کامپیوتری محاسبه کرد. این روش از متغیرهای ورودی شروع کرده و مشتق‌ها را به سمت خروجی تابع محاسبه می‌کند.

تابعی که در عکس میبینید با مثال متن متفاوت است. Computational graph of f(x1,x2,x3)=3*(x1**2+x2*x3) . در طول متن با مثال تصویری جدا و کتبی سعی میکنم مفهوم مشتق گیری اتوماتیک را توضیح بدهم.

با x و مشتق آن شروع کنید، که 1 است (زیرا مشتق x نسبت به x برابر با 1 است.

   x = x, dx/dx = 1

   تفکیک گام‌به‌گام:

   1. a = x, da/dx = 1

   2. b = a^2, db/dx = 2a * da/dx = 2a

   3. c = 3a, dc/dx = 3 * da/dx = 3

   4. d = b + c, dd/dx = db/dx + dc/dx = 2a + 3

   5. f(x) = d + 5, df/dx = dd/dx = 2a + 3

  
و a را دوباره به عنوان x جایگزین کنید:

   df/dx = 2x + 3

پس, تفکیک خودکار تابع را به قسمت‌های کوچکتر تقسیم می‌کند.

این فرآیند مشتق‌ها را گام‌به‌گام محاسبه می‌کند و آن‌ها را با استفاده از قاعده‌ی زنجیره‌ای ترکیب می‌کند.

برای تابع ما f(x) = x^2 + 3x + 5، AutoDiff به ما کمک می‌کند تا دریابیم که مشتق آن 2x + 3 است.

این فرآیند دقیق و کارآمد است و برای کامپیوتر‌ها برای مدیریت توابع پیچیده عالی است!

تفکیک خودکار حالت عقب( روش معکوس)

تفکیک خودکار روش معکوس به ویژه هنگام کار با توابعی که دارای چندین ورودی و یک خروجی هستند، بسیار مفید است، که در یادگیری ماشینی رایج است. بیایید این را با یک مثال تابع ساده شامل متغیرهای غیر اسکالر توضیح دهیم.

مثال تابع:

در نظر بگیرید یک تابع برداری ساده داریم

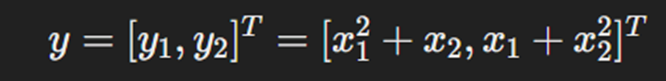
مراحل تفکیک خودکار روش معکوس

تجزیه تابع:

هر عملیات در تابع را شناسایی کرده و به صورت متغیرهای میانی نمایش دهید.

تابع ما می‌تواند به مراحل ساده‌تری تقسیم شود:

a1 = x1^2

a2 = x2

y1 = a1 + a2

b1 = x1

b2 = x2^2

y2 = b1 + b2

 مرحله جلو:

متغیرهای میانی و خروجی‌های نهایی را محاسبه کنید.

برای x = [x1, x2]^T:

a1 = x1^2

a2 = x2

y1 = a1 + a2

b1 = x1

b2 = x2^2

y2 = b1 + b2

مرحله عقب:

مشتقات را به ترتیب معکوس با استفاده از قانون زنجیره محاسبه کنید.

مشتقات خروجی نسبت به خود را به عنوان 1 مقداردهی اولیه کنید:

dy1/dy1 = 1, dy2/dy2 = 1

مشتقات متغیرهای میانی را محاسبه کنید:

dy1/da1 = 1, dy1/da2 = 1

dy2/db1 = 1, dy2/db2 = 1

با استفاده از قانون زنجیره، مشتقات را به ورودی‌ها x بازگردانید:

da1/dx1 = 2x1, da2/dx2 = 1

db1/dx1 = 1, db2/dx2 = 2x2

dy1/dx1 = dy1/da1 * da1/dx1 + dy1/da2 * da2/dx2 = 1 * 2x1 + 1 * 0 = 2x1

dy1/dx2 = dy1/da1 * da1/dx1 + dy1/da2 * da2/dx2 = 0 * 2x1 + 1 * 1 = 1

dy2/dx1 = dy2/db1 * db1/dx1 + dy2/db2 * db2/dx2 = 1 * 1 + 0 * 0 = 1

dy2/dx2 = dy2/db1 * db1/dx1 + dy2/db2 * db2/dx2 = 0 * 0 + 1 * 2x2 = 2x2

 بیاید با یک مثال دیگر به صورت تصویری هم این مراحل رو ببینیم

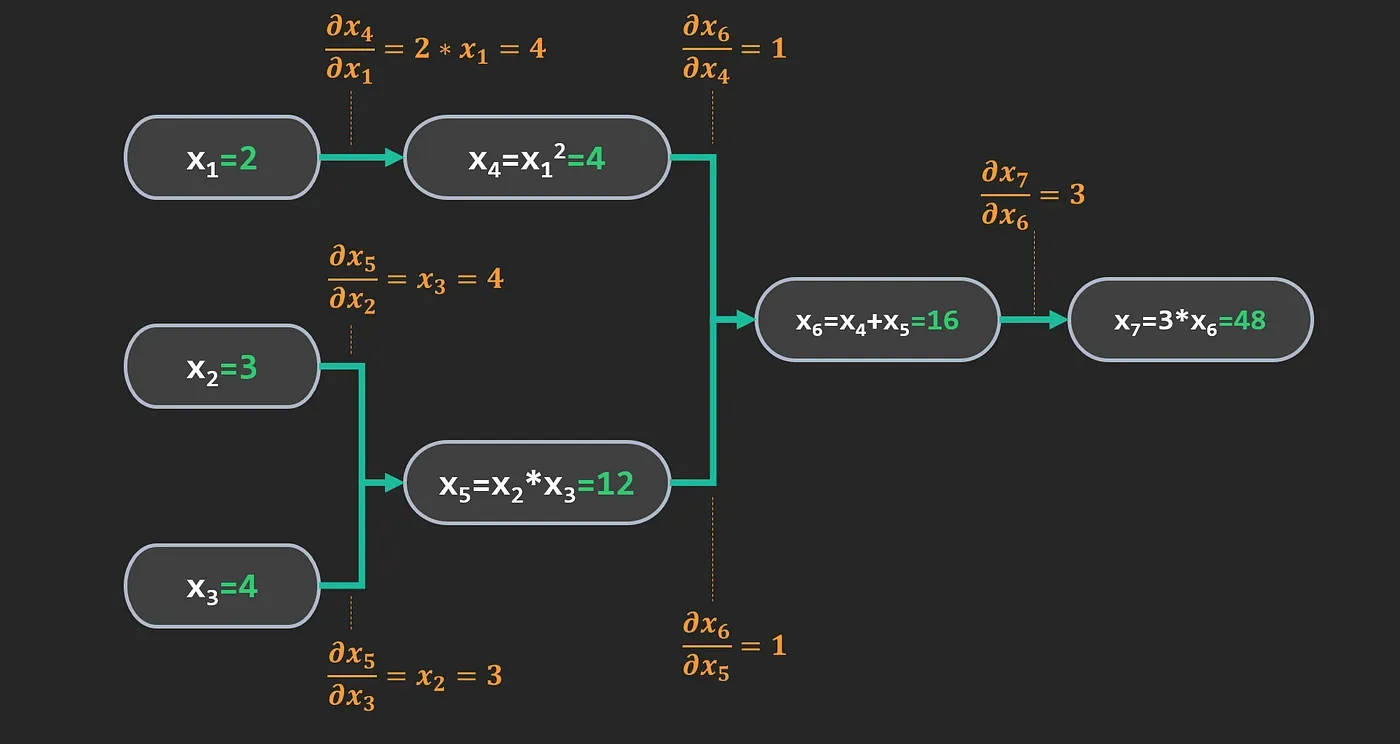
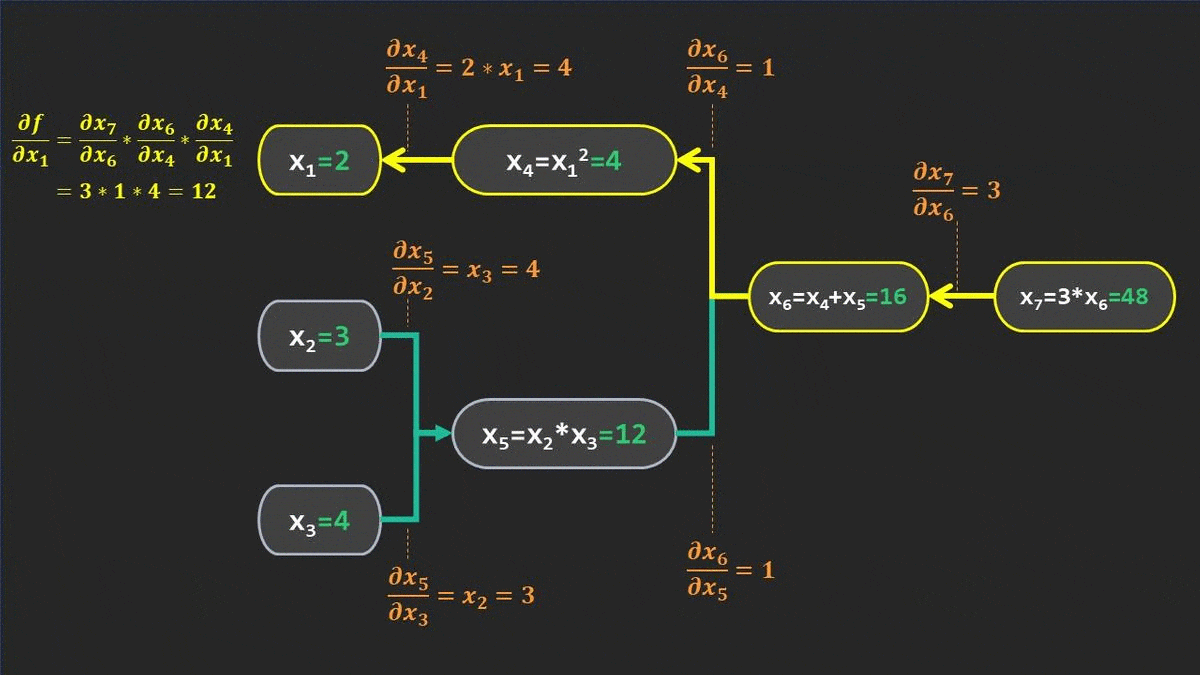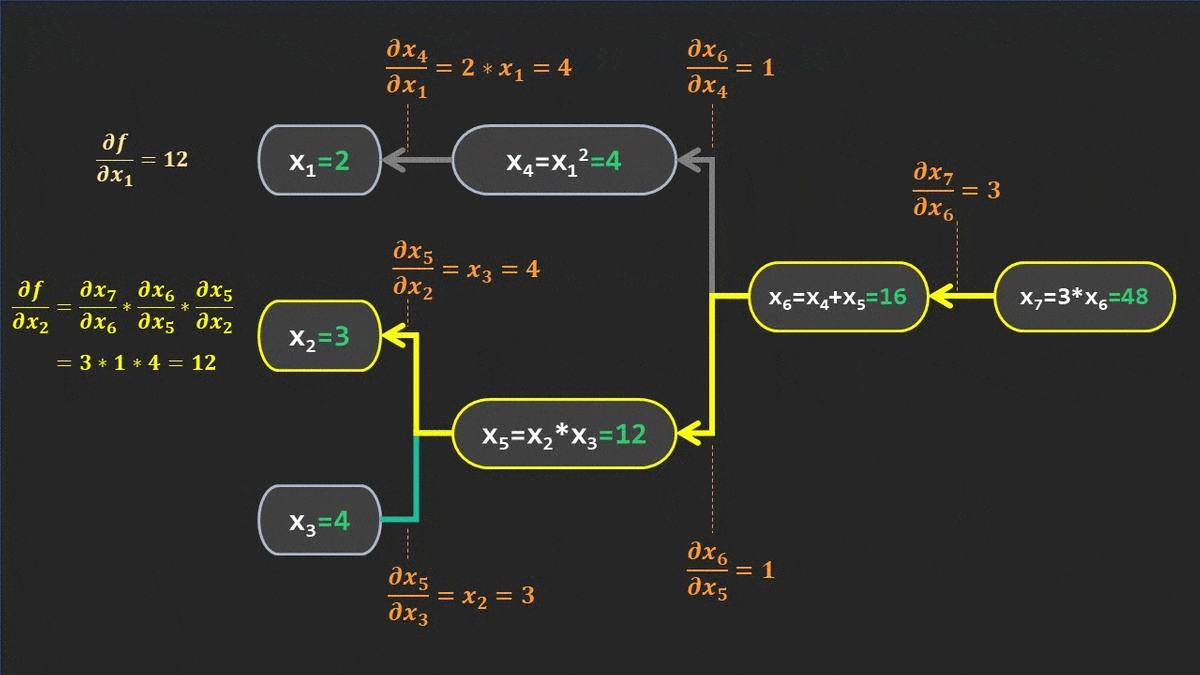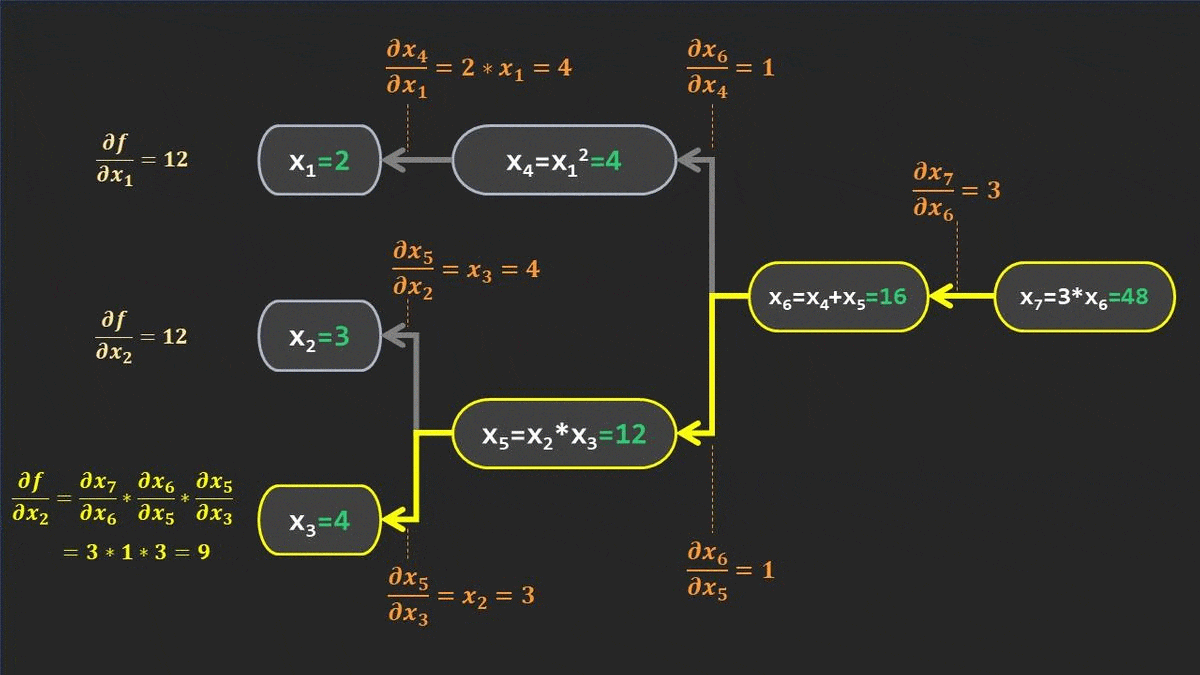
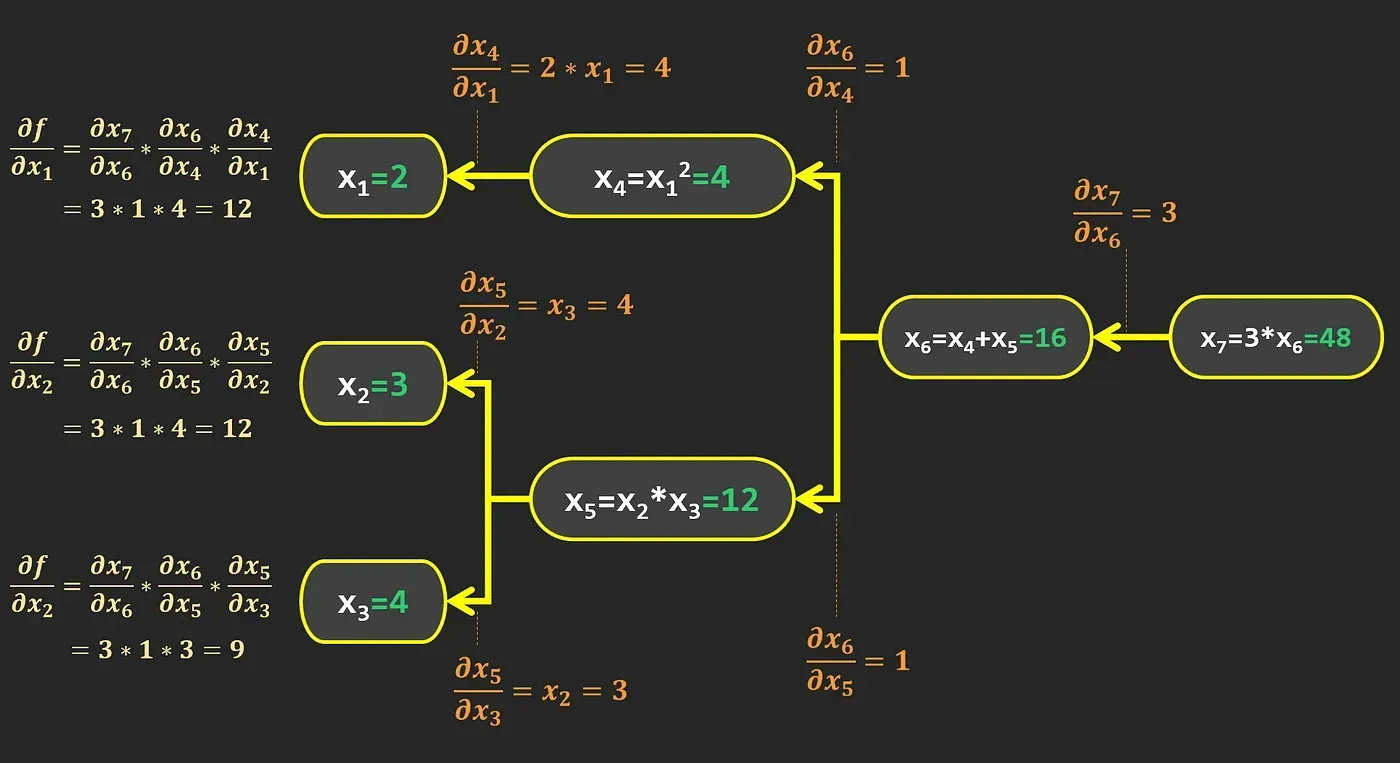
خلاصه

تفکیک خودکار حالت عقب مشتقات را از خروجی به ورودی محاسبه می‌کند.

این روش برای توابعی با بسیاری از ورودی‌ها و یک خروجی کارآمد است.

برای تابع برداری ما، مشتقات به صورت زیر محاسبه می‌شوند:

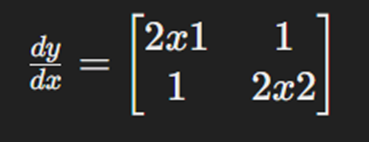
جداسازی محاسبات در دیفرانسیل خودکار :( Detaching Computation Automatic Differentiation)

دیفرانسیل خودکار با استفاده از تکنیک جداسازی محاسبات به ما امکان می‌دهد تا بخش‌هایی از گراف محاسباتی را از محاسبه گرادیان‌ها حذف کنیم. این کار هنگامی مفید است که بخواهیم مقادیر خاصی را ثابت نگه داریم و در طول فرآیند آموزش به‌روزرسانی نکنیم.

توضیح ساده

۱. مثال تابع:

فرض کنید تابعی به صورت f(x) = (x^2 + y^2) دارید و می‌خواهید مشتق آن را نسبت به x محاسبه کنید، اما نه نسبت به y.

۲. جداسازی:

وقتی شما یک متغیر را "جدا" می‌کنید، به کامپیوتر می‌گویید که آن را هنگام محاسبه گرادیان‌ها در نظر نگیرد.

در مثال ما، اگر y جدا شود، محاسبه گرادیان نحوه تغییرات y را نادیده می‌گیرد.

۳. چرا از جداسازی استفاده می‌کنیم:

مقادیر ثابت: گاهی اوقات، شما می‌خواهید برخی متغیرها ثابت باقی بمانند. جداسازی اطمینان می‌دهد که این متغیرها به‌روزرسانی نشوند.

ساده‌سازی محاسبات: این کار می‌تواند محاسبات را ساده‌تر و سریع‌تر کند.

۴. مثال در عمل:

اگر y در تابع f(x) = (x^2 + y^2) جدا شود:

گرادیان نسبت به x به طور عادی محاسبه می‌شود: df/dx = 2x.

گرادیان نسبت به y نادیده گرفته می‌شود زیرا y جدا شده است.

ترکیب گرادیان‌ها و کنترل جریان در پایتون

گرادیان‌ها به ما کمک می‌کنند تا درک کنیم تغییر در ورودی‌ها چگونه بر خروجی‌ها تأثیر می‌گذارد و در یادگیری ماشین برای بهینه‌سازی توابع کلیدی هستند. کنترل جریان در پایتون از دستوراتی مانند if، for، و while برای هدایت ترتیب عملیات در کد استفاده می‌کند.

import torch

def example_function(x):

    y = 0

    for i in range(5):

        if i % 2 == 0:

            y += x ** 2

        else:

            y += x

    return y

x = torch.tensor(2.0, requires_grad=True)

y = example_function(x)

y.backward()

print(x.grad) 

#این دستور گرادیان y نسبت به x را چاپ می‌کند

توضیحات

تعریف تابع:

تابع example_function(x) پنج بار حلقه می‌زند.

برای i زوج x^2 و برای i فرد x به y اضافه می‌شود.

محاسبه گرادیان:

x یک تانسور است که گرادیان‌ها را پیگیری می‌کند (requires_grad=True).

y = example_function(x) مقدار y را محاسبه می‌کند.

y.backward() گرادیان y نسبت به x را محاسبه می‌کند.

print(x.grad) گرادیان را نشان می‌دهد.

نکات کلیدی:

کنترل جریان (for و if) تغییر می‌دهد که چگونه x در محاسبات استفاده می‌شود.

گرادیان تمام این مشارکت‌ها را از هر حلقه و شرایط منعکس می‌کند.

گرادیان (Gradient)

گرادیان یکی از مفاهیم مهم در حساب دیفرانسیل و انتگرال است که در تحلیل توابع چندمتغیره به کار می‌رود. گرادیان یک بردار است که جهت و میزان بیشترین افزایش یک تابع را نشان می‌دهد.

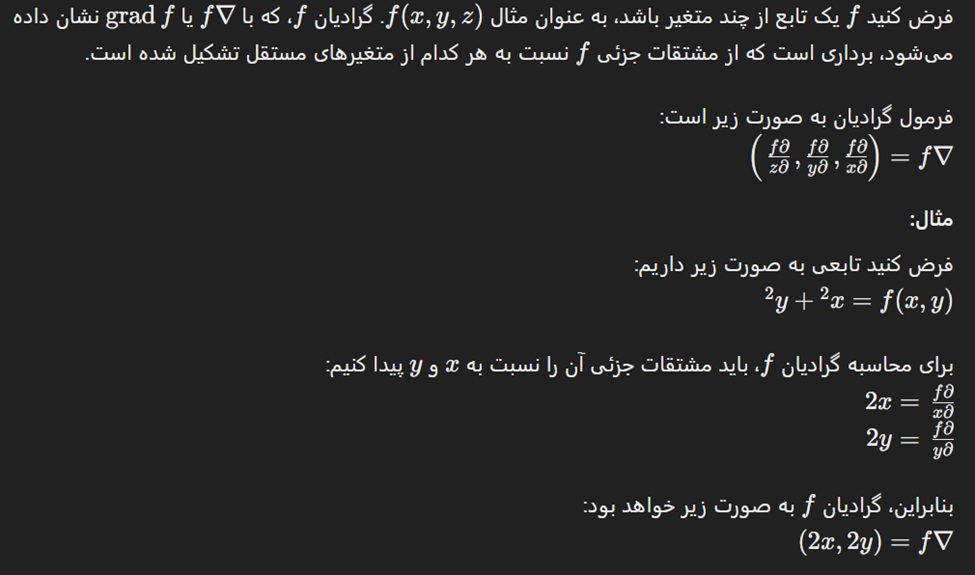
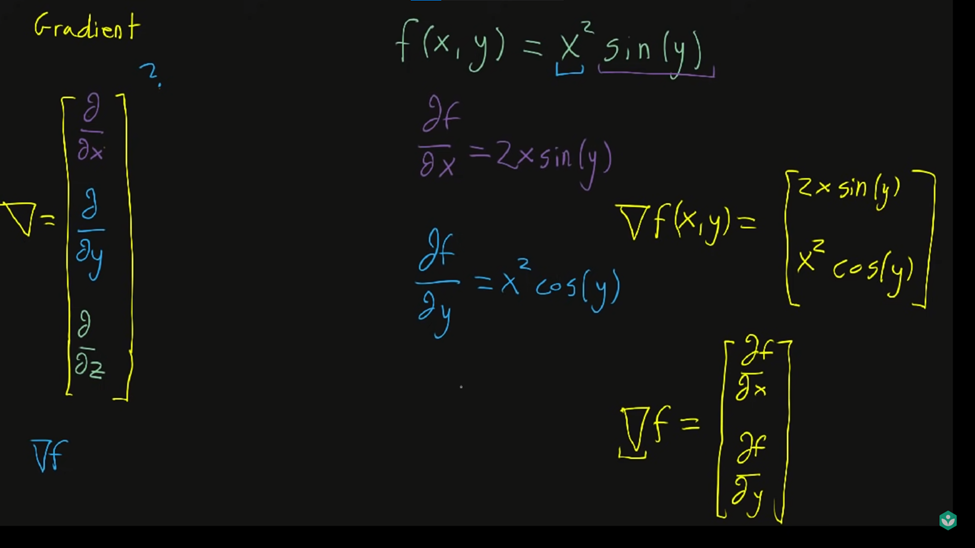
تصویر نشان می‌دهد که گرادیان چگونه از مشتقات جزئی تشکیل می‌شود و با استفاده از یک مثال ساده، نحوه محاسبه گرادیان یک تابع دو متغیره f(x,y)را توضیح می‌دهد. این گرادیان نشان‌دهنده جهت و میزان بیشترین افزایش تابع در فضای چندمتغیره است.

 نتیجه‌گیری

مشتق‌گیری اتوماتیک (AutoDiff) روشی قدرتمند و دقیق برای محاسبه مشتقات توابع با استفاده از برنامه‌های کامپیوتری است. این روش با تحلیل مستقیم کدهای تابع، مشتقات را به صورت مرحله‌به‌مرحله محاسبه می‌کند و از دقت بالا و کارایی بیشتری نسبت به روش‌های عددی و نمادین برخوردار است. استفاده از مشتق‌گیری اتوماتیک در یادگیری ماشین، بهینه‌سازی و مدل‌سازی ریاضی و فیزیکی بسیار مفید است و به ما کمک می‌کند تا مسائل پیچیده را به سادگی و دقت بالا حل کنیم.

پی‌نوشت

استفاده از مشتق‌گیری اتوماتیک در یادگیری ماشین و بهینه‌سازی به‌طور چشمگیری افزایش یافته است و این روش به یکی از ابزارهای اصلی در تحلیل و بهبود مدل‌های پیچیده تبدیل شده است. همچنین، این روش به مهندسان و محققان امکان می‌دهد تا با بهره‌گیری از قدرت کامپیوترها، به دقت و سرعت بالاتری در محاسبات مشتقات دست یابند.

برای اطلاعات یبشتر پیشنهاد میکنم این مقاله کوتاه را مطالعه بکنید https://medium.com/@rhome/automatic-differentiation-26d5a993692b 

راه‌های ارتباط:

ایمیل:     bita.nf@gmail.com

لینکدین : www.linkedin.com/in/bita-farahmand-58363a232

توییتر:      BitaBloom@