حساب دیفرانسیل و انتگرال شاخه‌ای از ریاضیات است که به مطالعه نرخ تغییرات و تجمع می‌پردازد. این شاخه شامل دو بخش اصلی دیفرانسیل و انتگرال است. دیفرانسیل به بررسی مشتقات و نرخ تغییرات لحظه‌ای توابع می‌پردازد، در حالی که انتگرال به محاسبه مساحت زیر منحنی‌ها و تجمع مقادیر می‌پردازد. این مفاهیم در بسیاری از زمینه‌های علمی و مهندسی کاربرد دارند، از جمله فیزیک، اقتصاد، و مهندسی، که به تحلیل و حل مسائل پیچیده و مدل‌سازی پدیده‌های طبیعی کمک می‌کنند. حساب دیفرانسیل و انتگرال ابزارهای اساسی برای درک و توصیف دنیای پیرامون ما را فراهم می‌کند.

مشتق و دیفرانسیل:

مشتق نشان‌دهنده تغییرات یک تابع با تغییر ورودی آن است. به طور رسمی‌تر، مشتق یک تابع f(x) در نقطه x به عنوان حد تعریف می‌شود:

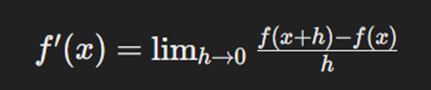
این حد، اگر وجود داشته باشد، شیب خط مماس به نمودار تابع f در نقطه x را می‌دهد.

دیفرانسیل گیری فرآیند یافتن مشتق یک تابع است. در زیر برخی از فرمول‌ها و مثال‌های دیفرانسیل گیری آورده شده است: 

ابزارهای تصور(Visualization Utilities)

ابزارهای تصوردر حساب دیفرانسیل و انتگرال به ما کمک می‌کنند تا مفاهیم پیچیده ریاضی را بهتر درک کنیم. این ابزارها شامل نمودارها، گراف‌ها، و نرم‌افزارهای مختلفی هستند که نمایش بصری از توابع، مشتقات، انتگرال‌ها و دیگر مفاهیم ریاضی ارائه می‌دهند.

برخی از ابزارهای تصورمتداول:

1.   نمودارهای دوبعدی (2D Graphs): این نمودارها به ما کمک می‌کنند تا رفتار توابع را در دو بعد مشاهده کنیم. مثلاً نمودار تابع f(x) نشان می‌دهد که چگونه مقدار تابع با تغییرات xxx تغییر می‌کند. همچنین، با اضافه کردن خطوط مماس به نمودار، می‌توان مشتقات و نرخ تغییرات را مشاهده کرد.

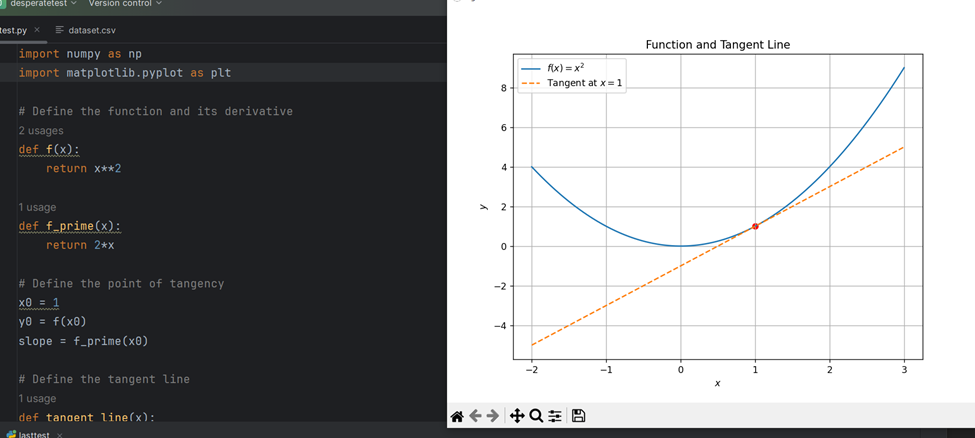
مثال: نمودار تابع f(x) = x^2f و مشتق آن f′(x)=2xf'(x)  .

2.   نمودارهای سه‌بعدی (3D Graphs): برای توابع چند متغیره مانند f(x, y) ، نمودارهای سه‌بعدی می‌توانند نمایش بصری بهتری از سطح‌ها و نقاط بحرانی ارائه دهند. این نمودارها به ما کمک می‌کنند تا مفهوم مشتقات جزئی و گرادیان‌ها را بهتر درک کنیم.

مثال: نمودار سه‌بعدی تابع f(x, y) = x^2 + y^2

3.   نرم‌افزارهای ریاضی (Mathematical Software): نرم‌افزارهایی مانند MATLAB، Mathematica، و GeoGebra ابزارهای قدرتمندی برای تصورو تحلیل ریاضی ارائه می‌دهند. این نرم‌افزارها می‌توانند نمودارهای پیچیده، انتگرال‌ها، مشتقات و دیگر محاسبات ریاضی را به راحتی رسم و تجزیه و تحلیل کنند.

4.   نمودارهای تعاملی (Interactive Graphs): وب‌سایت‌ها و ابزارهای آنلاین مانند Desmos به کاربران اجازه می‌دهند تا به صورت تعاملی با توابع و نمودارها کار کنند. این ابزارها به دانشجویان و دانش‌آموزان کمک می‌کنند تا با تغییر پارامترها و مشاهده نتایج، مفاهیم ریاضی را بهتر درک کنند.

مزایا:

• درک بهتر مفاهیم: تصور به درک بهتر و سریع‌تر مفاهیم پیچیده ریاضی کمک می‌کند.
• آموزش و یادگیری: ابزارهای تجسم برای آموزش و یادگیری ریاضیات بسیار مفید هستند و به دانش‌آموزان کمک می‌کنند تا مفاهیم را به صورت عمیق‌تر و با لذت بیشتری یاد بگیرند.
• تحلیل داده‌ها: در تحقیقات علمی و مهندسی، تصورداده‌ها به محققان کمک می‌کند تا الگوها و روندهای مهم را شناسایی کنند و نتایج دقیق‌تری به دست آورند.

با استفاده از این ابزارها، می‌توانیم به صورت بصری و تعاملی با مفاهیم پیچیده حساب دیفرانسیل و انتگرال آشنا شویم و درک بهتری از آن‌ها پیدا کنیم.

برای مثال، با استفاده از پایتون و Matplotlib: کد زیر تابع f(x)=x^2 و خط مماس آن در x=1 را تجسم می‌کند: 

قاعده زنجیره‌ای (Chain Rule)

قاعده زنجیره‌ای یکی از مهم‌ترین قواعد در حساب دیفرانسیل و انتگرال است که برای مشتق‌گیری از توابع مرکب استفاده می‌شود. این قاعده به ما اجازه می‌دهد تا مشتق یک تابع مرکب را با استفاده از مشتقات توابع ساده‌تر محاسبه کنیم.

فرمول این فرمول نشان می‌دهد که برای یافتن مشتق تابع مرکب، باید ابتدا مشتق 𝑓 را نسبت به 𝑔(𝑥) محاسبه کنیم و سپس آن را در مشتق 𝑔 نسبت به 𝑥 ضرب کنیم.

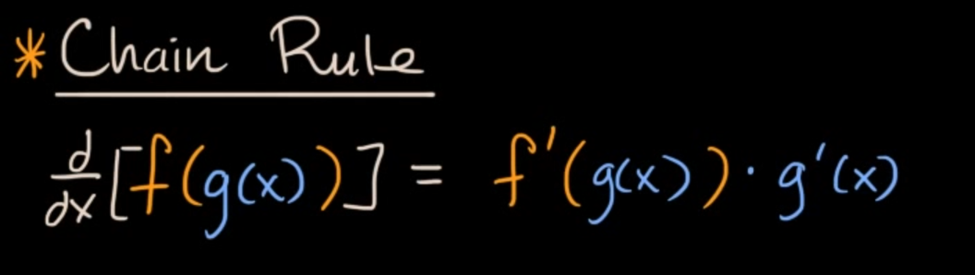
نتیجه‌گیری

حساب دیفرانسیل و انتگرال با مطالعه نرخ تغییرات و تجمع، به تحلیل و پیش‌بینی رفتار سیستم‌های پیچیده کمک می‌کند. دیفرانسیل به بررسی مشتقات و تغییرات لحظه‌ای توابع می‌پردازد، در حالی که انتگرال مساحت زیر منحنی‌ها و تجمع مقادیر را محاسبه می‌کند. این مفاهیم در بسیاری از زمینه‌های علمی و مهندسی کاربرد دارند.

پی‌نوشت

مشتق تغییرات یک تابع را با تغییر ورودی آن نشان می‌دهد و دیفرانسیل‌گیری فرآیند یافتن مشتق است. ابزارهای تجسم مانند نمودارها و نرم‌افزارهای ریاضی به درک بهتر این مفاهیم کمک می‌کنند. قاعده زنجیره‌ای نیز برای مشتق‌گیری از توابع مرکب استفاده می‌شود و مشتق تابع مرکب را با استفاده از مشتقات توابع ساده‌تر محاسبه می‌کند.

راه‌های ارتباط:

ایمیل:     bita.nf@gmail.com

لینکدین : www.linkedin.com/in/bita-farahmand-58363a232

توییتر:      BitaBloom@