مرور کلی جبر خطی
جبر خطی یکی از پایههای اساسی ریاضیات مدرن است و کاربردهای آن در زمینههای مختلفی از جمله علوم کامپیوتر، فیزیک و مهندسی گسترده است. این پست به توضیح مفاهیم کلیدی جبر خطی میپردازد و پایهای محکم برای مطالعه بیشتر فراهم میکند.
جبر خطی یکی از پایههای اساسی ریاضیات مدرن است و کاربردهای آن در زمینههای مختلفی از جمله علوم کامپیوتر، فیزیک و مهندسی گسترده است. این پست به توضیح مفاهیم کلیدی جبر خطی میپردازد و پایهای محکم برای مطالعه بیشتر فراهم میکند.
اسکالرها
یک اسکالر یک عدد واحد است. مثالهایی شامل مقادیری مانند ۵ کیلوگرم یا ۳۰ درجه سانتیگراد است. در نماد تانسور، اسکالرها تانسورهای رتبه صفر هستند.
بردارها
یک بردار مقداری است که هم اندازه و هم جهت دارد. مثالهایی شامل ۱۰ متر بر ثانیه به سمت شمال یا ۲۰ نیوتن به سمت پایین است. در علوم کامپیوتر، بردارها لیستهای مرتبی از اعداد هستند و به عنوان تانسورهای رتبه ۱ شناخته میشوند.
ماتریسها
یک ماتریس یک آرایه دو بعدی از اعداد است که در سطرها و ستونها چیده شدهاند. ماتریسها تانسورهای رتبه ۲ هستند و در جبر خطی برای نمایش تبدیلهای خطی و سیستمهای معادلات خطی استفاده میشوند.
تانسورها
تانسورها تعمیمی از اسکالرها، بردارها و ماتریسها به ابعاد بالاتر هستند. آنها آرایههای چند بعدی از اعداد هستند. عملیاتهای اساسی روی تانسورها شامل موارد زیر است:
visualizing tensors
more on understanding tensors
۱. جمع
تعریف: اضافه کردن عناصر متناظر دو تانسور با شکل یکسان.
ویژگیها: جابجایی و شرکتپذیری.
A+B=B+A
(A+B)+C=A+(B+C)
۲. ضرب اسکالری
تعریف: ضرب هر عنصر از یک تانسور در یک اسکالر.
ویژگیها: توزیعپذیری بر روی جمع تانسور و شرکتپذیری با ضرب اسکالر.
α(A+B)=αA+αB
(α+β)A=αA+βA
α(βA)=(αβ)A
۳. ضرب عنصری (محصول هادامارد)
تعریف: ضرب عناصر متناظر دو تانسور با شکل یکسان.
ویژگیها: جابجایی و شرکتپذیری.
A⊙B=B⊙A
(A⊙B)⊙C=A⊙(B⊙C)
۴. ضرب تانسور (ماتریس)
- تعریف: تعمیم ضرب ماتریس به تانسورها. حاصلضرب دو ماتریس A و B تعریف شده است اگر تعداد ستونهای A برابر با تعداد سطرهای B باشد.
- ویژگی: شرکتپذیر و توزیعپذیر، اما نه جابجایی.
A×(B×C)=(A×B)×C
A×(B+C)=A×B+A×C
۵. ترانهاده ماتریس
- تعریف: چرخاندن یک ماتریس روی قطر آن، جابجایی سطرها با ستونها.
- ویژگی: (A^T)^T = A, (A + B)^T = A^T + B^T, و (AB)^T = B^T A^T
Reduction(فرمهای کاهش در جبر خطی)
فرم سطری اکلون (REF)
یک ماتریس در فرم سطری اکلون قرار دارد اگر:
تمام سطرهای غیر صفر بالای سطرهای شامل همه صفرها قرار داشته باشند.
ورودی برجسته (محور) هر سطر غیر صفر ۱ باشد.
محور در هر سطر به سمت راست محور در سطر بالاتر قرار دارد.
فرم کاهشیافته سطری اکلون (RREF)
یک ماتریس در فرم RREF قرار دارد اگر:
1. در فرم REF باشد.
2. محور در هر سطر تنها ورودی غیر صفر در ستون خود باشد.

فرم قطری
یک ماتریس مربعی در فرم قطری است اگر تمام عناصر غیر قطری آن صفر باشند.
برای یک ماتریسA، آن را میتوان به فرم قطری D تبدیل کرد جایی که D = PAP^{-1} و P یک ماتریس وارونپذیر است.
کاربرد: سادهسازی عملیاتهای ماتریسی مانند ضرب ماتریسها و یافتن توانهای ماتریسها.

فرم مثلثی
یک ماتریس مربعی در فرم مثلثی (بالایی یا پایینی) قرار دارد اگر تمام عناصر زیر (مثلث بالایی) یا بالای (مثلث پایینی) قطر اصلی صفر باشند. این فرم برای حل سیستمهای خطی با استفاده از جانشینی رو به جلو یا عقب مفید است.

فرم جردن
فرم جردن یک ماتریس به شکل بلوکی قطری است که هر بلوک، یک بلوک جردن است. بلوکهای جردن ماتریسهایی هستند که عناصر روی قطر اصلی یکسان و عناصر بالای قطر اصلی یک و بقیه صفر هستند.
تجزیه ها
تجزیه مقدار منفرد (SVD)
تجزیه مقدار منفرد (SVD) یک تکنیک در جبر خطی است که یک ماتریس داده شده A را به سه ماتریس خاص تجزیه میکند و بینشهایی در مورد ویژگیها و ساختار ماتریس اصلی ارائه میدهد. این به صورت A=UΣV^T بیان میشود:
- A ماتریس اصلی با ابعاد m×n است.
- U یک ماتریس ارتوگونال m×m است. ستونهای آن بردارهای چپ منفرد A هستند.
- Σ یک ماتریس قطری m×n با اعداد حقیقی غیرمنفی روی قطر آن است. این اعداد، مقادیر منفرد A هستند.
- V^T ترانهاده یک ماتریس ارتوگونال n×n به نام V است. ستونهای آن بردارهای راست منفرد A هستند.
تجزیه LU
تعریف: یک ماتریس A را به حاصلضرب یک ماتریس مثلثی پایینی L و یک ماتریس مثلثی بالایی U تجزیه میکند. کاربرد: سادهسازی حل سیستمهای معادلات خطی، محاسبه دترمینانها، و وارونسازی ماتریسها.
تجزیه QR
تجزیه QR یک ماتریس را به حاصلضرب یک ماتریس ارتوگونال Q و یک ماتریس مثلثی بالایی R تجزیه میکند. این تجزیه به ویژه برای حل معادلات خطی و مسائل کمترین مربعات مورد استفاده قرار میگیرد.
ضرب ها
ضرب نقطهای
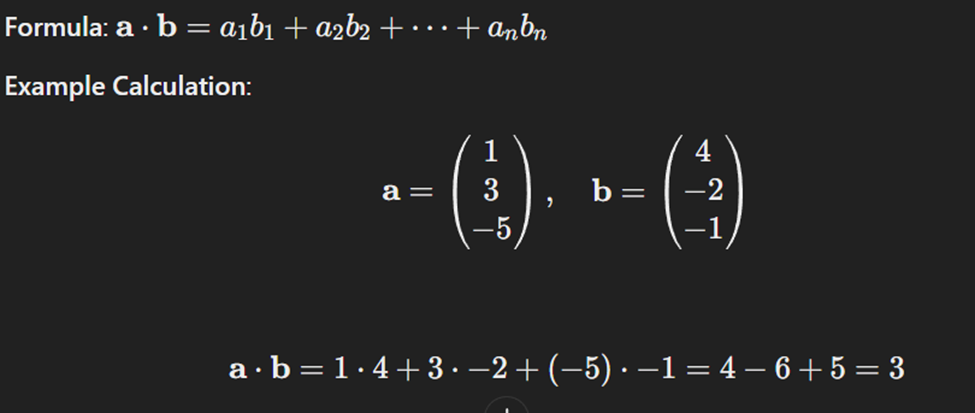
محصول ماتریس-بردار
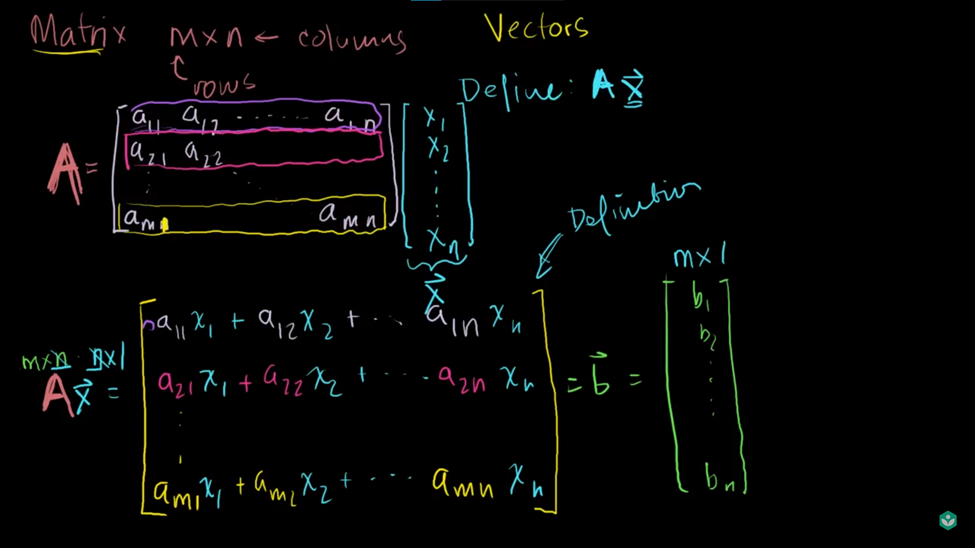
ما همچنین میتوانیم به هر ستون در ماتریس به عنوان یک بردار نگاه کنیم.
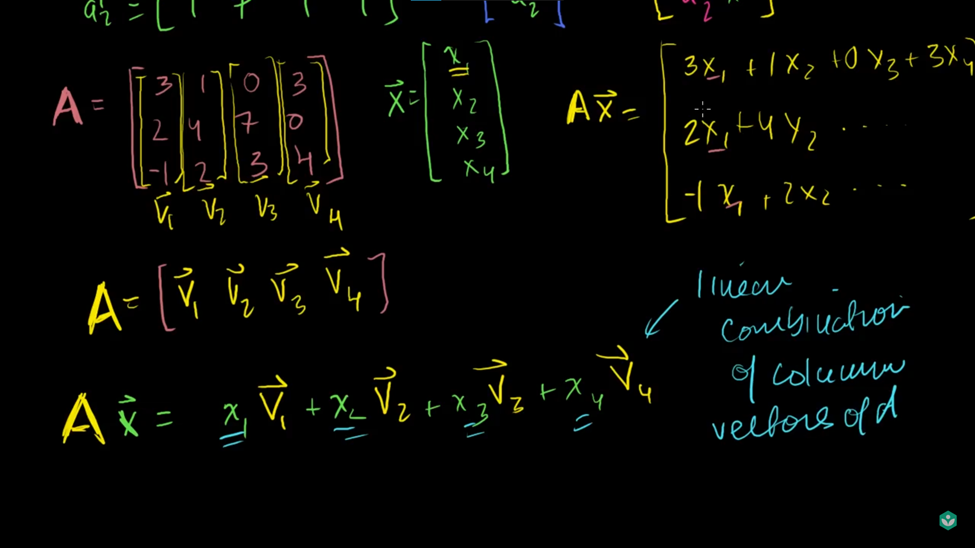
محصول ماتریس-بردار
ضرب ماتریس-ماتریس
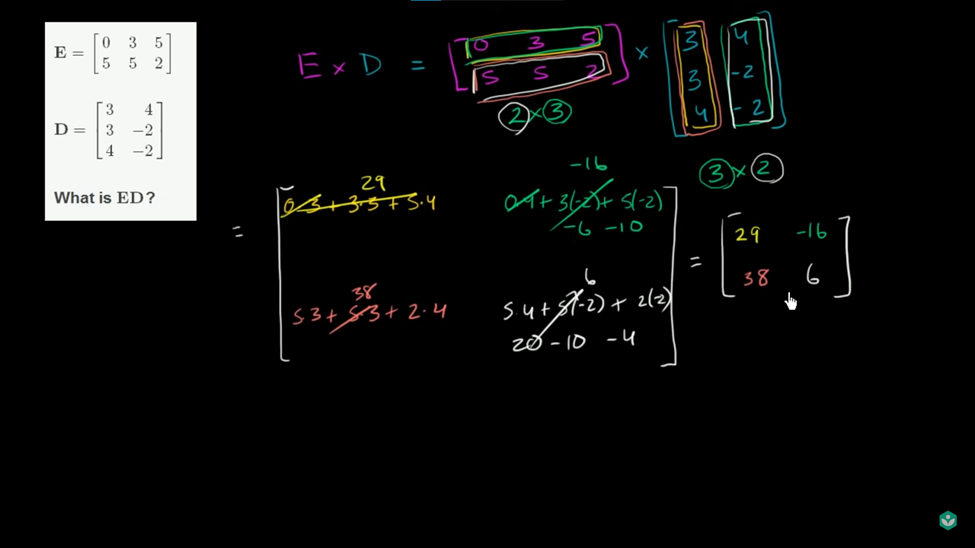
ضرب ماتریس-ماتریس
نُرمها در جبر خطی
نُرمهای بردار
نُرمها اندازه یا طول یک بردار را اندازهگیری میکنند.

نُرمهای ماتریس
نُرم ۱ : برای نُرم ۱، ما جمع مطلق ستونها را محاسبه میکنیم و بیشترین مقدار را انتخاب میکنیم
نُرم بینهایت: و برای بینهایت، ما از سطرها استفاده میکنیم

نُرمهای ماتریس
نتیجه گیری
با تسلط بر این مفاهیم اساسی، شما به خوبی مجهز خواهید بود تا به موضوعات پیشرفتهتر جبر خطی بپردازید و آنها را در مسائل مختلف علمی و مهندسی به کار بگیرید.
پینوشت
جبر خطی، یکی از پایههای اصلی ریاضیات و علوم کامپیوتر، ابزارهای قدرتمندی برای مدلسازی و حل مسائل پیچیده ارائه میدهد. از تحلیل دادهها و یادگیری ماشین گرفته تا مدلهای فیزیکی و مهندسی، جبر خطی نقش مهمی ایفا میکند. درک مفاهیم اساسی مانند اسکالرها، بردارها، ماتریسها و تانسورها و عملیاتهای مختلف روی آنها، پایهای قوی برای پیشرفت در این زمینه فراهم میکند.
راههای ارتباط:
ایمیل: bita.nf@gmail.com
لینکدین : www.linkedin.com/in/bita-farahmand-58363a232
توییتر: BitaBloom@
