احتمال به میزان وقوع رویدادها اشاره دارد. وقتی یک رویداد رخ می‌دهد، مانند پرتاب یک توپ، انتخاب یک کارت از یک دسته، و غیره، باید یک احتمال با آن رویداد مرتبط باشد. از نظر ریاضیات، احتمال به نسبت نتایج مطلوب به تعداد کل نتایج ممکن اشاره دارد.

احتمال یک رویداد

 اگر تعداد کل نتایج ممکن یک آزمایش تصادفی p باشد و q از آن‌ها نتایج مطلوب برای رویداد A باشند، آنگاه احتمال رویداد A با P(A) نشان داده می‌شود و به صورت زیر محاسبه می‌شود:

P(A) = q/p

احتمال عدم وقوع رویداد

 A، یعنی P(A’) برابر است با:

P(A’) = 1 – P(A)

نکته

اگر مقدار P(A) = 1 باشد، رویداد A یک رویداد قطعی نامیده می‌شود.

اگر مقدار P(A) = 0 باشد، رویداد A یک رویداد غیرممکن نامیده می‌شود.

همچنین، P(A) + P(A’) = 1

فرمول احتمال

می‌گوید که احتمال وقوع یک رویداد برابر است با نسبت تعداد نتایج مطلوب به تعداد کل نتایج ممکن.

احتمال وقوع رویداد P(E) = تعداد نتایج مطلوب / تعداد کل نتایج ممکن

فرض کنید A، B و C رویدادهای مرتبط با یک آزمایش تصادفی هستند، آنگاه:

P(A∪B) = P(A) + P(B) – P(A∩B)

P(A∪B) = P(A) + P(B)                                                                                                   اگر A و B متقابلاً ناسازگار باشند.    

P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) – P(B∩C)- P(C∩A) + P(A∩B∩C)

P(A∩B’) = P(A) – P(A∩B)

P(A’∩B) = P(B) – P(A∩B)

بسط قضیه ضرب – فرض کنید A1، A2، …، An رویدادهای مرتبط با یک آزمایش تصادفی هستند، آنگاه:

P(A1∩A2∩A3 ….. An) = P(A1)P(A2/A1)P(A3/A2∩A1) ….. P(An/A1∩A2∩A3∩ ….. ∩An-1)

احتمال پرتاب سکه

یک سکه دو طرف دارد، بنابراین دو نتیجه ممکن از یک پرتاب سکه‌ی منصفانه وجود دارد: رو (H) یا پشت (T).

فرمول احتمال پرتاب سکه

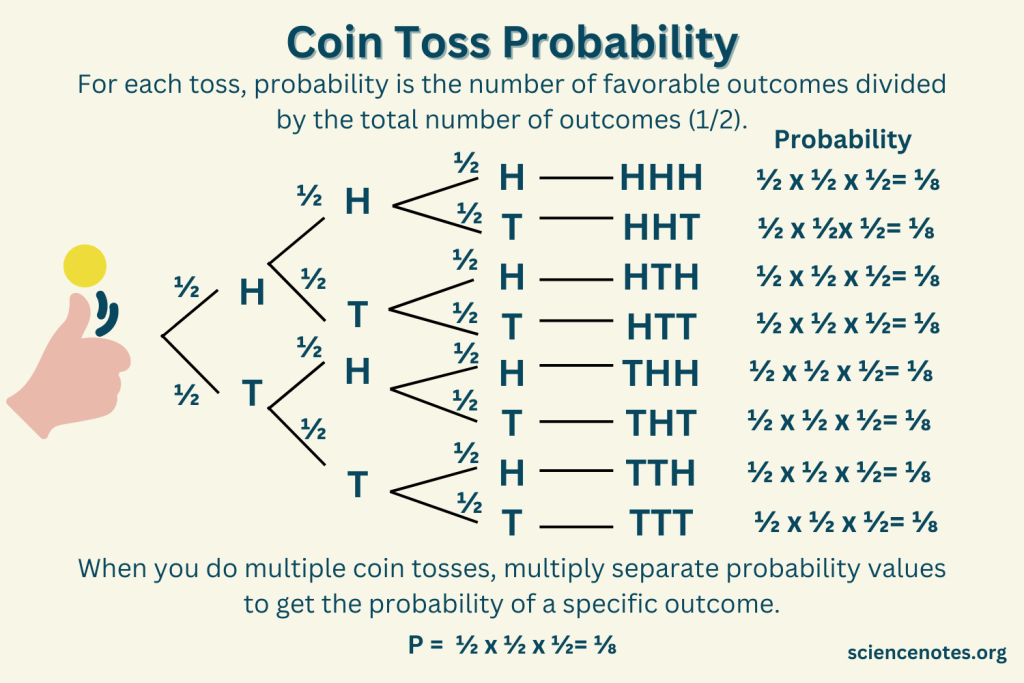
فرمول احتمال پرتاب سکه تعداد نتایج مطلوب تقسیم بر تعداد کل نتایج ممکن است. برای یک سکه، این محاسبه آسان است زیرا تنها دو نتیجه ممکن وجود دارد. آمدن رو یک نتیجه است. آمدن پشت نتیجه دیگر است.

حتمال آمدن یا رو یا پشت (۲ نتیجه ممکن) برابر با ۱ است. به عبارت دیگر، هنگامی که یک سکه را پرتاب می‌کنید، تقریباً تضمین شده که یا رو یا پشت خواهد آمد.

P=2/2​=1

آمدن رو یا پشت روی یک سکه، رویدادهای متقابلاً ناسازگار هستند. اگر رو بیاید، پشت نمی‌آید (و بالعکس). روش دیگری برای محاسبه احتمال دو رویداد متقابلاً ناسازگار جمع کردن احتمالات فردی آن‌ها است. برای یک پرتاب سکه:

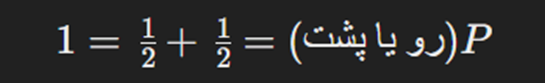
احتمال برای چندین پرتاب سکه

اگر سکه را بیش از یک بار پرتاب کنید و بخواهید احتمال یک نتیجه خاص را محاسبه کنید، باید مقادیر احتمال هر پرتاب را در هم ضرب کنید. این روش زمانی کار می‌کند که پرتاب‌ها رویدادهای مستقل باشند. به این معنی که نتیجه پرتاب دوم (یا سوم و غیره) وابسته به نتیجه پرتاب اول (یا هر پرتاب قبلی یا بعدی) نیست.

برای مثال، بیایید احتمال آمدن رو، رو، پشت (HHT) را محاسبه کنیم:

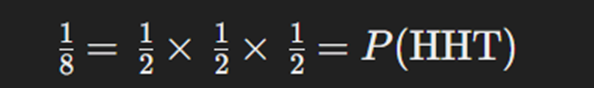
برای درک جامع تر پیبشنهاد میکنم این ویدیو را ببینید:

مثال ساده: پرتاب سکه‌ها: بر اساس لینک ویدیو ارائه شده، در اینجا مثالی با دو رویکرد مختلف آورده شده است.

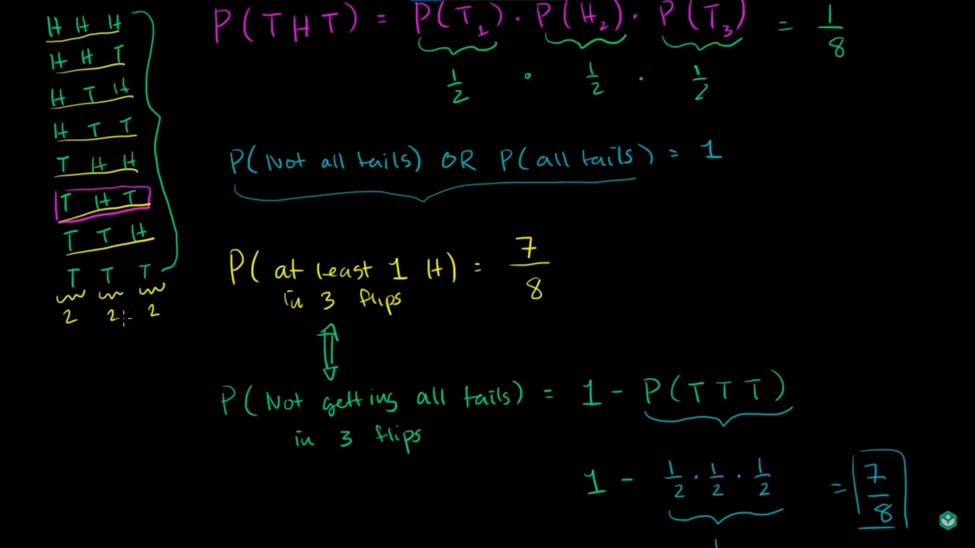
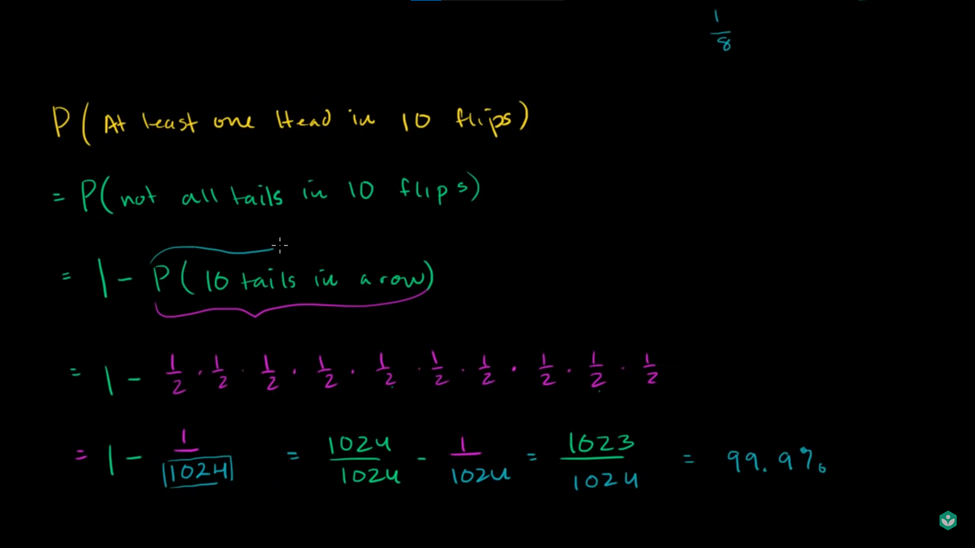
مرور دوباره بر قوانین احتمال:

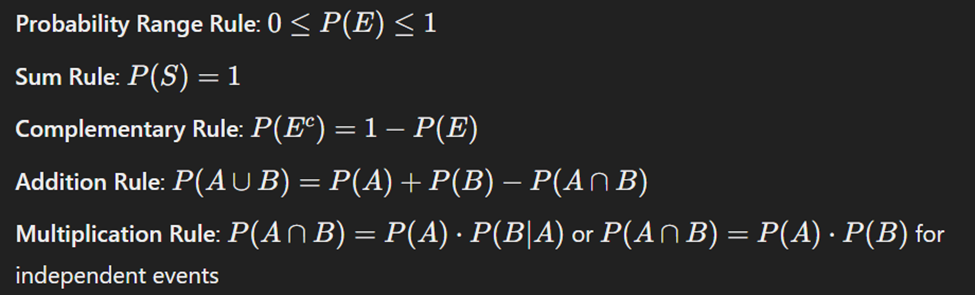
متغیرهای تصادفی و چندین متغیر تصادفی در احتمال و آمار

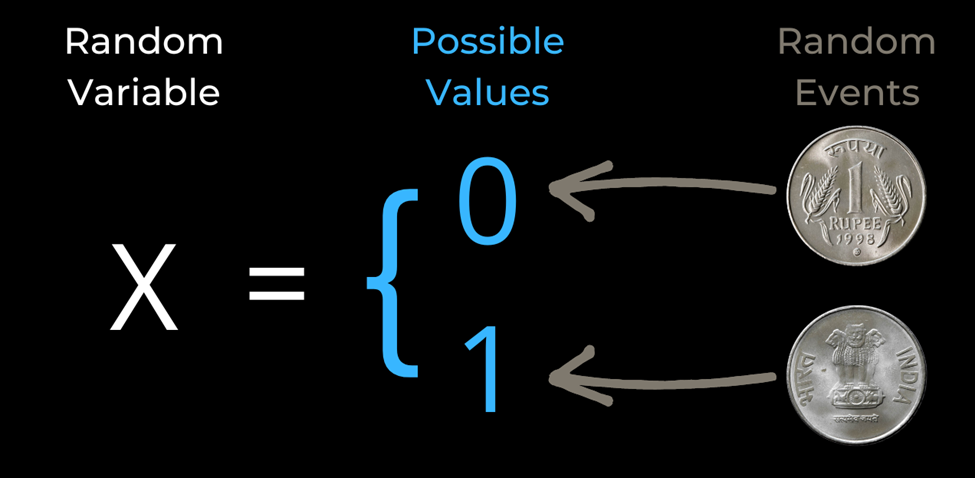
متغیر تصادفی یک متغیر است که بر اساس نتیجه یک رویداد تصادفی مقادیر مختلفی می‌گیرد. دو نوع متغیر تصادفی وجود دارد:

 گسسته و پیوسته.

متغیرهای تصادفی گسسته

متغیرهای تصادفی گسسته می‌توانند تعداد محدودی از مقادیر مجزا را بپذیرند. یک آزمایش را در نظر بگیرید که در آن سکه‌ای سه بار پرتاب می‌شود. اگر X تعداد بارهایی که سکه به رو می‌آید را نشان دهد، در این صورت X یک متغیر تصادفی گسسته است که می‌تواند فقط مقادیر 0، 1، 2 یا 3 را داشته باشد (از هیچ بار رو آمدن سکه در سه پرتاب متوالی تا هر سه بار رو آمدن سکه). هیچ مقدار دیگری برای X ممکن نیست.

متغیرهای تصادفی پیوسته

متغیرهای تصادفی پیوسته می‌توانند هر مقداری را در یک محدوده یا بازه مشخص بپذیرند و می‌توانند تعداد بی‌نهایتی از مقادیر ممکن را بپذیرند. یک مثال از متغیر تصادفی پیوسته می‌تواند یک آزمایش باشد که شامل اندازه‌گیری میزان بارندگی در یک شهر در طول یک سال یا میانگین قد یک گروه تصادفی از 25 نفر باشد.

با توجه به مثال اخیر، اگر Y نشان دهنده متغیر تصادفی برای میانگین قد یک گروه تصادفی از 25 نفر باشد، نتیجه به دست آمده یک مقدار پیوسته خواهد بود زیرا قد می‌تواند 5 فوت، 5.01 فوت یا 5.0001 فوت باشد. به وضوح، تعداد بی‌نهایتی از مقادیر ممکن برای قد وجود دارد.

متغیرهای تصادفی پیوسته رایج

برخی از توزیع‌های رایج که در آن‌ها از متغیر تصادفی پیوسته استفاده می‌شود عبارتند از:

·       توزیع یکنواخت

·       توزیع نرمال

·       توزیع نمایی

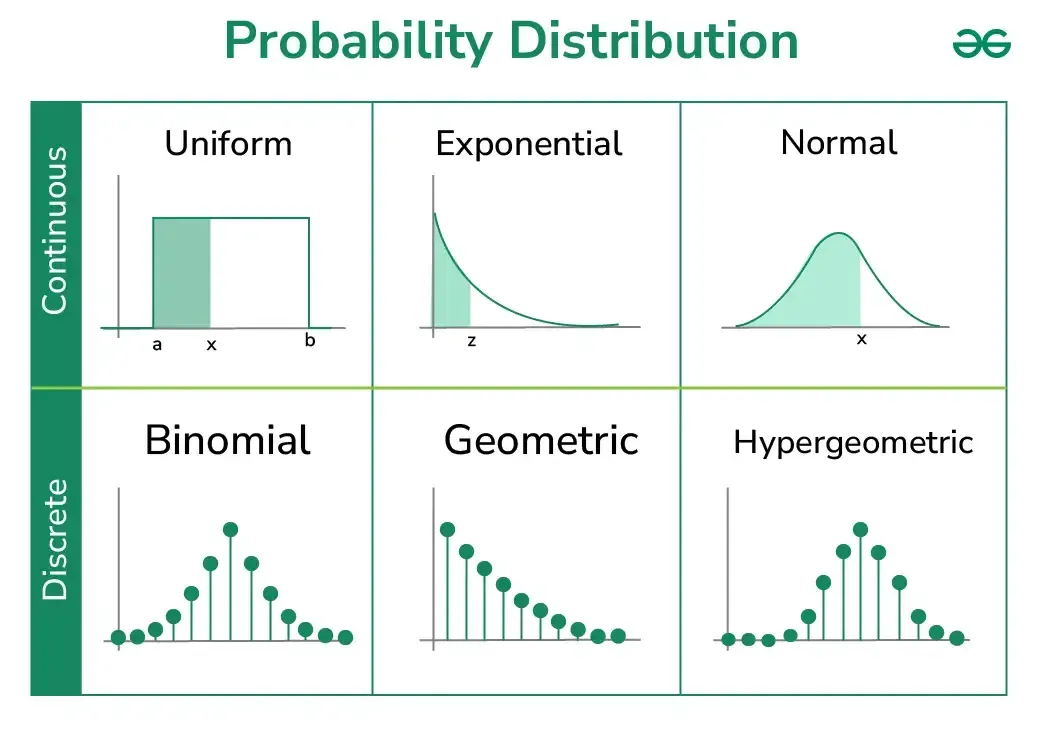
توزیع یکنواخت

یک متغیر تصادفی پیوسته X بین a و b به صورت یکنواخت توزیع شده است اگر تابع چگالی احتمال (PDF) آن به صورت زیر باشد:

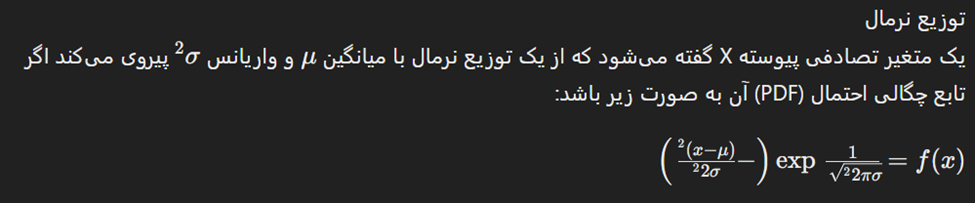
توزیع نرمال

توزیع نمایی

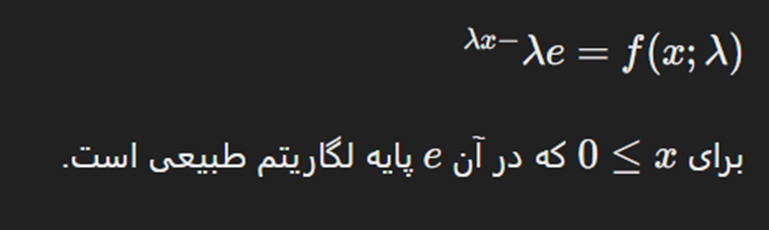
توزیع نمایی یک توزیع احتمال پیوسته است که برای مدل‌سازی زمان بین رویدادها در فرایندی که در آن رویدادها به طور پیوسته و مستقل با نرخ متوسط ثابتی رخ می‌دهند، استفاده می‌شود. این توزیع توسط پارامتر نرخ  λ مشخص می‌شود که نرخ وقوع رویدادها را تعریف می‌کند. تابع چگالی احتمال (PDF) توزیع نمایی به صورت زیر داده می‌شود:

توجه: علاوه بر این‌ها، برخی دیگر از توزیع‌ها که در آن‌ها متغیر تصادفی پیوسته مفید است عبارتند از:

• توزیع گاما
• توزیع بتا
• توزیع کای-دو (Chi-Square)
• توزیع t استیودنت

امید ریاضی    (Expected Value)

امید ریاضی یا مقدار مورد انتظار، میانگین وزنی تمامی مقادیر ممکن یک متغیر تصادفی است که با توجه به احتمال وقوع هر مقدار محاسبه می‌شود. به عبارتی، امید ریاضی نشان‌دهنده میانگین نتایج یک آزمایش در صورت تکرار بی‌نهایت بار است.

واریانس (Variance)

واریانس میزان پراکندگی مقادیر یک متغیر تصادفی از میانگین آن را نشان می‌دهد. به عبارتی، واریانس نشان‌دهنده میزان تفاوت مقادیر یک متغیر تصادفی با میانگین آن است. واریانس به صورت میانگین مجذور فاصله‌ها از میانگین تعریف می‌شود.

برای متغیر تصادفی گسستهX، واریانس به صورت زیر محاسبه می‌شود:

امید ریاضی نشان‌دهنده میانگین مقادیر ممکن یک متغیر تصادفی است.

واریانس میزان پراکندگی و تفاوت مقادیر یک متغیر تصادفی از میانگین آن را نشان می‌دهد.

احتمال شرطی

احتمال وقوع یک رویداد با فرض وقوع رویداد دیگر. به صورت P(A|B) نشان داده می‌شود که به معنای "احتمال A با فرض B" است.

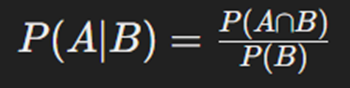
خلاصه:

این متن به بررسی مفاهیم اساسی در احتمال و آمار می‌پردازد. در این متن، فرمول‌های مربوط به احتمال وقوع و عدم وقوع یک رویداد، احتمالات مرکب و شرطی، و همچنین مفاهیم متغیرهای تصادفی گسسته و پیوسته مورد بررسی قرار گرفته‌اند. همچنین، توضیح داده شده که چگونه این مفاهیم در توزیع‌هایی مانند توزیع نمایی، نرمال و یکنواخت به کار می‌روند.

پی‌نوشت:

مفاهیم احتمال و آمار کاربردهای فراوانی در زمینه‌های مختلف دارند، از تحلیل داده‌ها و مدل‌سازی علمی گرفته تا تصمیم‌گیری‌های روزمره و حل مسائل پیچیده. دانش این مباحث نه تنها برای دانشمندان داده بلکه برای هر کسی که به دنبال درک بهتر از پدیده‌های تصادفی و پیش‌بینی رویدادها است، ارزشمند است. 

 منابع:

https://sciencenotes.org/coin-toss-probability-formula-and-examples/

https://www.geeksforgeeks.org/random-variable/

راه‌های ارتباط:

ایمیل:     bita.nf@gmail.com

لینکدین : www.linkedin.com/in/bita-farahmand-58363a232

توییتر:      BitaBloom@